الكلمات كالتالي استمع إليها بالترتيب من خلال ناطق قوقل الموجود اسفل الترجمة:
هل لاحظت شيء؟
إنما يفعله الألمان كما نفعله في اللغة العربية، ننطق الآحاد ثم العشرات، فتنطق كلمة Dreiundzwanzig كما ننطقها نحن في النظير العربي “ثلاثة و عشرون” وليس كنظير باقي اللغات “عشرون و ثلاثة”. هذا ما أخذه الألمان آنذاك وذلك لأنهم قد أخذوا هذه العادة من عند العرب في نطق الأرقام، فكانوا بالبداية ينطقونها كما ينطقها الإنجليز ولكن تأثروا الألمان في نطقها كما ينطقها العرب في كتبهم وذلك لما مر فيهم من مرحلة انتقال من الأرقام الرومانية إلى الأرقام العربية- وبالأساس الهندية-.
حكاية الأرقام
مرت الأرقام في أحوال عديدة وأشكال مختلفه فمرورا من الفينيقيين والعبرانيين إلى الإغريق وحتى الرومانيين فكانت الأرقام لاتزال لا تعبر في صيغتها الكتابية كما هي في النطق، فكان دائما ما يسهل نطقها ولكن تصعب كتابتها فكلي تكتب ١٨٨٨ ستكون هكذا MDCCCLXXXVIII = 1000 + 500 + 100 + 100 + 100 + 50 + 10 + 10 + 10 + 5 + 1 + 1 + 1
فكل هذه الرموز من اجل التعبير عن رقم بسيط وقد كانت محدوديتها تصعب مع الأرقام الكبيرة والعمليات الحسابية.
بدأت حكاية الأرقام العربية -الهندية- في الهند، حيث خرجت الهند من النظام الذي يستعمله الإغريق والرومان وضعوا لكل رقم ترميز من الآحاد ولكن كانت المشكلة هو انك لا تستطيع التفرقة إذ ما أن الأرقام تتبع العشرات أم الآحاد فمثلا يصعب كتابة الرقم 604 لعدم وجود شيء يبين أن كانت الخانة تميل إلى المئات أم العشرات. إن الهند كانوا في عام 300ق.م وحتى القرن السادس يستعملون كتابة الأرقام مع ترميز معين مثلا كتابة الرقم 1358 كالتالي 8آ 5ع 3م 1أ (8 آحاد، 5عشرات، 3مئات، 1ألوف ).
من اهم إسهامات المسلمون في عالم الأرقام كانت تتلخص في علم الحساب والجبر و الهندسة وعلم المثلثات و الفلك “علم الهيئة”.
الحساب
كان كما قصصنا لكم القصة أعلاة وهو إدخالهم الأرقام العربية الشرقية “١٢٣٤٥٦٧٨٩” و الأرقام العربية الغربية “123456789″ والتي سادت من بلاد الأندلس ثم انتقلت إلى أوروبا. و وجد علماء المسلمين طريقة الإحصاء العشري كما انهم أوجدوا الفاصلة للكسر العشري وهذا الفضل يرجع إلى العالم غياث الدين الكاشي.
الجبر
وهذا يعد من ابرز ما قدمه المسلمون في هذه العلوم إذ انه لازال يحتفظ باسمه. الجبر ببساطه أن تستخرج القيم المجهولة من المعطيات المعلومة”-التعريف من عندي :D-. وقد عرف هذا العلم البابليون ولكن لم يكن علم ثابت راسخ وإنما مبعثرات من بين علماء الرياضيات وأيضا لم يكن لهم رموز لهذه العلوم.
أما المسلمون فقد وضعوا رموز لعلم الجبر مثل “جـ” للجذر و”س” للأس ..ألخ. كما انهم حلوا المعادلات من الدرجة الثانية والثالثة والرابعة وصنفوا المعادلات إلى ستة أقسام وجمعوا بين الهندسة والجبر و وضعوا أساس الهندسة التحليلية و التي كانت الطرق الممهدة لعلم التفاضل و التكامل.
معادلة من الدرجة الرابعة قبل عشرة قرون؟!
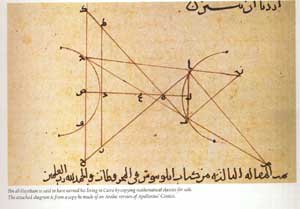
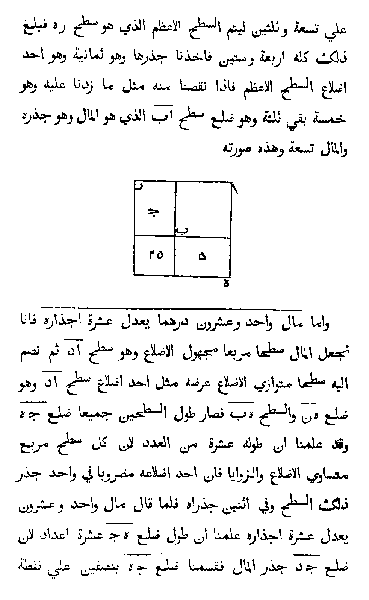
نـعم، لقد حل إبن الهيثم المسألة التي سميت باسمه وهي المسألة الهيثمية باستخدام معادلة من الدرجة الرابعة وإليكم أعزائي الرياضين هذه المسألة:
“ضم المجلد الخامس من كتابه المناظر مناقشة ما هو يعرف الآن بـ “مسألة ابن الهيثم”، التي صاغها بطليموس للمرة الأولى عام 150م، وهي تتألف من رسم خطّين من نقطتين على سطح دائرة ليجتمعا في نقطة على محيط الدائرة، ويصنعان زاويتين متساويتين مع المستوى العمودي على السطح عند تلك النقطة، وهو ما يشبه العثور على نقطة على حافة طاولة بلياردو دائرية التي تستهدفها الكرة الضاربة لضرب كرة أخرى في نقطة أخرى. وبالتالي، فإن التطبيق الرئيسي لهذه المسألة في علم البصريات هو “إذا كان لدينا مصدر ضوء ومرآة كروية، هو كيف نحدد النقطة على المرآة التي يتنعكس عليها الضوء لعين الناظر”، وهو ما قاده إلى معادلة من الدرجة الرابعة.[13][54] قاد ذلك مصادفةً ابن الهيثم لصياغة صيغة رياضية لجمع متوالية من القوة الرابعة، باستخدام طريقة بدائية من البرهان الرياضي بالاستقراء الرياضي، فاستنتج في النهاية طريقة يمكن استخدامها بسهولة للحصول على مجموع أي متواليات من قوى أكبر. استخدم ابن الهيثم طريقته في إيجاد مجموع متواليات القوى، لتحديد حجم سطح مكافئ من خلال التكامل. وبالتالي، تمكن من إجراء التكامل على كثيرات الحدود حتى الدرجة الرابعة، واقترب من التوصل إلى صيغة عامة للتكامل أي من كثيرات الحدود. كان ذلك أساسًا لتطوير علم تفاضل وتكامل متناهيات الصغر.[55] كما حل ابن الهيثم مسألته باستخدام الإقطاع المخروطية والإثباتات الهندسية، وعلى الرغم من أن العديد من بعده حاولوا إيجاد حلول جبرية لتلك المسائل،[56] إلا أنه لم يتم الوصول إلى الحل إلا في عام 1997 على يدي عالم الرياضيات في جامعة أكسفورد بيتر نيومان.[57]“. ويكيبيديا إبن الهيثم.
